Вирусная эпидемия не может просто так закончиться. Карантин, не карантин, самоизоляция или нет, но законы природы просто так не выключить. Можно например как в Китае, по приказу Коммунистической партии принять решение, что эпидемия закончена и выдавать в эфир ноль вновь зараженных, но далеко не все страны на это способны.
Однако с помощью науки и формул можно примерно предсказать временные рамки эпидемии на базе уже имеющихся данных или как сейчас модно говорить «на основании Big Data».
Вот что получилось у одного пытливого человека…
Согласно статистике, развитие эпидемий в мире происходит по нормальному закону распределения Гаусса. Берем его за основу.
y(t) = b · e -c·(t-a)2
Исходные данные ti — ежедневные отметки времени xi — число активных случаев болезни в этот день
Натуральный логарифм от y(t) и от данных xi
ui = ln(xi) u(t) = ln(y) = ln(b) — c·t2 + 2c·a·t — c·a2
Сделаем замены: А=-с; B=2a·c; C=ln(b)-c·a2; Получаем
u(t) = A·t2 + B·t + C
Чтобы найти А, В и С — использую метод наименьших квадратов, согласно которому сумма по i от 1 до n квадратов разностей
Σ(xi — y(ti))2 -> min
должна стремится к минимуму.
Назовем эту сумму Ф (A, В, С)
Продифференцируем dФ по dA, dB и dC. Производные при это должны быть равны нулю.
Получаем систему уравнений
A·Σti4 + B·Σti3 + C·Σti2 = Σui·ti2
A·Σti3 + B·Σti2 + C·Σti = Σui·ti
A·Σti2 + B·Σti + C·n = Σui
Решаем эту систему по методу Крамера
А = ∆A/∆
B = ∆B/∆
C = ∆C/∆
Находим нужные коэффициенты a, b , c для исходной функции
И, вуаля, готово! Программируем и рисуем красивые графики и узнаем когда это кончится!
Вот например график для России:
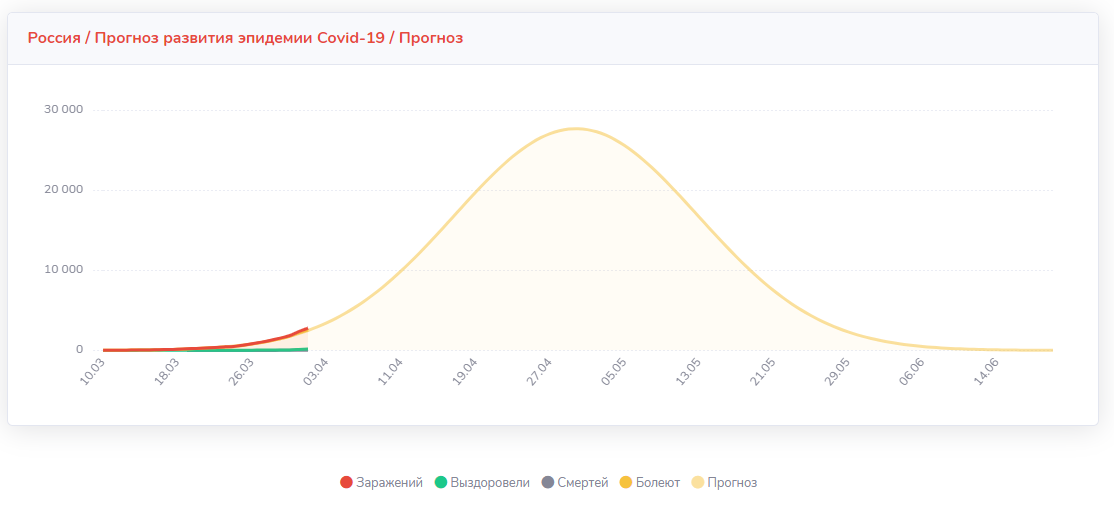
Чем больше данных, тем точнее прогноз. На данный момент, реальные данные экспертов в Италии говорят о пике эпидемии, и кривая Гаусса показывает тоже самое.

По ссылке ниже смотрите прогнозы для других стран и для всей планеты — https://coronavirussia.online/
https://tjournal.ru/science/155655-prognoz-pandemii-koronavirusa-normalnoe-raspredelenie